Hyperparameter tuning by grid-search¶

In the previous notebook, we saw that hyperparameters can affect the generalization performance of a model. In this notebook, we will show how to optimize hyperparameters using a grid-search approach.

Our predictive model¶

Let us reload the dataset as we did previously:

from sklearn import set_config

set_config(display="diagram")

import pandas as pd

adult_census = pd.read_csv("../datasets/adult-census.csv")

We extract the column containing the target.

target_name = "class"
target = adult_census[target_name]
target

       <=50K
       <=50K
        >50K
        >50K
       <=50K
          ...  
   <=50K
    >50K
   <=50K
   <=50K
    >50K
Name: class, Length: 48842, dtype: object

We drop from our data the target and the "education-num" column which duplicates the information from the "education" column.

data = adult_census.drop(columns=[target_name, "education-num"])
data.head()

	age	workclass	education	marital-status	occupation	relationship	race	sex	capital-gain	hours-per-week	native-country
0	25	Private	11th	Never-married	Machine-op-inspct	Own-child	Black	Male	0	40	United-States
1	38	Private	HS-grad	Married-civ-spouse	Farming-fishing	Husband	White	Male	0	50	United-States
2	28	Local-gov	Assoc-acdm	Married-civ-spouse	Protective-serv	Husband	White	Male	0	40	United-States
3	44	Private	Some-college	Married-civ-spouse	Machine-op-inspct	Husband	Black	Male	7688	40	United-States
4	18	?	Some-college	Never-married	?	Own-child	White	Female	0	30	United-States

Once the dataset is loaded, we split it into a training and testing sets.

from sklearn.model_selection import train_test_split

data_train, data_test, target_train, target_test = train_test_split(
    data, target, random_state=42)

We will define a pipeline as seen in the first module. It will handle both numerical and categorical features.

The first step is to select all the categorical columns.

from sklearn.compose import make_column_selector as selector

categorical_columns_selector = selector(dtype_include=object)
categorical_columns = categorical_columns_selector(data)

Here we will use a tree-based model as a classifier (i.e. HistGradientBoostingClassifier). That means:

Numerical variables don’t need scaling;
Categorical variables can be dealt with an OrdinalEncoder even if the coding order is not meaningful;
For tree-based models, the OrdinalEncoder avoids having high-dimensional representations.

We now build our OrdinalEncoder by passing it the known categories.

from sklearn.preprocessing import OrdinalEncoder

categorical_preprocessor = OrdinalEncoder(handle_unknown="use_encoded_value",
                                          unknown_value=-1)

We then use a ColumnTransformer to select the categorical columns and apply the OrdinalEncoder to them.

from sklearn.compose import ColumnTransformer

preprocessor = ColumnTransformer([
    ('cat-preprocessor', categorical_preprocessor, categorical_columns)],
    remainder='passthrough', sparse_threshold=0)

Finally, we use a tree-based classifier (i.e. histogram gradient-boosting) to predict whether or not a person earns more than 50 k$ a year.

# for the moment this line is required to import HistGradientBoostingClassifier
from sklearn.experimental import enable_hist_gradient_boosting
from sklearn.ensemble import HistGradientBoostingClassifier
from sklearn.pipeline import Pipeline

model = Pipeline([
    ("preprocessor", preprocessor),
    ("classifier",
     HistGradientBoostingClassifier(random_state=42, max_leaf_nodes=4))])
model

Pipeline

Pipeline(steps=[('preprocessor',
                 ColumnTransformer(remainder='passthrough', sparse_threshold=0,
                                   transformers=[('cat-preprocessor',
                                                  OrdinalEncoder(handle_unknown='use_encoded_value',
                                                                 unknown_value=-1),
                                                  ['workclass', 'education',
                                                   'marital-status',
                                                   'occupation', 'relationship',
                                                   'race', 'sex',
                                                   'native-country'])])),
                ('classifier',
                 HistGradientBoostingClassifier(max_leaf_nodes=4,
                                                random_state=42))])

preprocessor: ColumnTransformer

ColumnTransformer(remainder='passthrough', sparse_threshold=0,
                  transformers=[('cat-preprocessor',
                                 OrdinalEncoder(handle_unknown='use_encoded_value',
                                                unknown_value=-1),
                                 ['workclass', 'education', 'marital-status',
                                  'occupation', 'relationship', 'race', 'sex',
                                  'native-country'])])

cat-preprocessor

['workclass', 'education', 'marital-status', 'occupation', 'relationship', 'race', 'sex', 'native-country']

OrdinalEncoder

OrdinalEncoder(handle_unknown='use_encoded_value', unknown_value=-1)

remainder

passthrough

passthrough

HistGradientBoostingClassifier

HistGradientBoostingClassifier(max_leaf_nodes=4, random_state=42)

Tuning using a grid-search¶

In the previous exercise we used one for loop for each hyperparameter to find the best combination over a fixed grid of values. GridSearchCV is a scikit-learn class that implements a very similar logic with less repetitive code.

Let’s see how to use the GridSearchCV estimator for doing such search. Since the grid-search will be costly, we will only explore the combination learning-rate and the maximum number of nodes.

%%time
from sklearn.model_selection import GridSearchCV

param_grid = {
    'classifier__learning_rate': (0.01, 0.1, 1, 10),
    'classifier__max_leaf_nodes': (3, 10, 30)}
model_grid_search = GridSearchCV(model, param_grid=param_grid,
                                 n_jobs=2, cv=2)
model_grid_search.fit(data_train, target_train)

CPU times: user 1.66 s, sys: 132 ms, total: 1.79 s
Wall time: 8.9 s

GridSearchCV

GridSearchCV(cv=2,
             estimator=Pipeline(steps=[('preprocessor',
                                        ColumnTransformer(remainder='passthrough',
                                                          sparse_threshold=0,
                                                          transformers=[('cat-preprocessor',
                                                                         OrdinalEncoder(handle_unknown='use_encoded_value',
                                                                                        unknown_value=-1),
                                                                         ['workclass',
                                                                          'education',
                                                                          'marital-status',
                                                                          'occupation',
                                                                          'relationship',
                                                                          'race',
                                                                          'sex',
                                                                          'native-country'])])),
                                       ('classifier',
                                        HistGradientBoostingClassifier(max_leaf_nodes=4,
                                                                       random_state=42))]),
             n_jobs=2,
             param_grid={'classifier__learning_rate': (0.01, 0.1, 1, 10),
                         'classifier__max_leaf_nodes': (3, 10, 30)})

preprocessor: ColumnTransformer

ColumnTransformer(remainder='passthrough', sparse_threshold=0,
                  transformers=[('cat-preprocessor',
                                 OrdinalEncoder(handle_unknown='use_encoded_value',
                                                unknown_value=-1),
                                 ['workclass', 'education', 'marital-status',
                                  'occupation', 'relationship', 'race', 'sex',
                                  'native-country'])])

cat-preprocessor

['workclass', 'education', 'marital-status', 'occupation', 'relationship', 'race', 'sex', 'native-country']

OrdinalEncoder

OrdinalEncoder(handle_unknown='use_encoded_value', unknown_value=-1)

remainder

passthrough

passthrough

HistGradientBoostingClassifier

HistGradientBoostingClassifier(max_leaf_nodes=4, random_state=42)

Finally, we will check the accuracy of our model using the test set.

accuracy = model_grid_search.score(data_test, target_test)
print(
    f"The test accuracy score of the grid-searched pipeline is: "
    f"{accuracy:.2f}"
)

The test accuracy score of the grid-searched pipeline is: 0.88

Warning

Be aware that the evaluation should normally be performed in a cross-validation framework by providing model_grid_search as a model to the cross_validate function.

Here, we are using a single train-test split to highlight the specificities of the model_grid_search instance. We will show such examples in the last section of this notebook.

The GridSearchCV estimator takes a param_grid parameter which defines all hyperparameters and their associated values. The grid-search will be in charge of creating all possible combinations and test them.

The number of combinations will be equal to the product of the number of values to explore for each parameter (e.g. in our example 4 x 3 combinations). Thus, adding new parameters with their associated values to be explored become rapidly computationally expensive.

Once the grid-search is fitted, it can be used as any other predictor by calling predict and predict_proba. Internally, it will use the model with the best parameters found during fit.

Get predictions for the 5 first samples using the estimator with the best parameters.

model_grid_search.predict(data_test.iloc[0:5])

array([' <=50K', ' <=50K', ' >50K', ' <=50K', ' >50K'], dtype=object)

You can know about these parameters by looking at the best_params_ attribute.

print(f"The best set of parameters is: "
      f"{model_grid_search.best_params_}")

The best set of parameters is: {'classifier__learning_rate': 0.1, 'classifier__max_leaf_nodes': 30}

The accuracy and the best parameters of the grid-searched pipeline are similar to the ones we found in the previous exercise, where we searched the best parameters “by hand” through a double for loop.

In addition, we can inspect all results which are stored in the attribute cv_results_ of the grid-search. We will filter some specific columns from these results.

cv_results = pd.DataFrame(model_grid_search.cv_results_).sort_values(
    "mean_test_score", ascending=False)
cv_results.head()

	mean_fit_time	std_fit_time	mean_score_time	std_score_time	param_classifier__learning_rate	param_classifier__max_leaf_nodes	params	split0_test_score	split1_test_score	mean_test_score	std_test_score	rank_test_score
5	0.613430	0.052576	0.263728	0.000364	0.1	30	{'classifier__learning_rate': 0.1, 'classifier...	0.868912	0.867213	0.868063	0.000850	1
4	0.478177	0.018796	0.238310	0.009586	0.1	10	{'classifier__learning_rate': 0.1, 'classifier...	0.866783	0.866066	0.866425	0.000359	2
7	0.169529	0.012972	0.108432	0.003592	1	10	{'classifier__learning_rate': 1, 'classifier__...	0.854826	0.862899	0.858863	0.004036	3
6	0.222120	0.035791	0.120544	0.008352	1	3	{'classifier__learning_rate': 1, 'classifier__...	0.853844	0.860934	0.857389	0.003545	4
3	0.348125	0.007120	0.168634	0.005148	0.1	3	{'classifier__learning_rate': 0.1, 'classifier...	0.852752	0.853781	0.853266	0.000515	5

Let us focus on the most interesting columns and shorten the parameter names to remove the "param_classifier__" prefix for readability:

# get the parameter names
column_results = [f"param_{name}" for name in param_grid.keys()]
column_results += [
    "mean_test_score", "std_test_score", "rank_test_score"]
cv_results = cv_results[column_results]

def shorten_param(param_name):
    if "__" in param_name:
        return param_name.rsplit("__", 1)[1]
    return param_name


cv_results = cv_results.rename(shorten_param, axis=1)
cv_results

	learning_rate	max_leaf_nodes	mean_test_score	std_test_score	rank_test_score
5	0.1	30	0.868063	0.000850	1
4	0.1	10	0.866425	0.000359	2
7	1	10	0.858863	0.004036	3
6	1	3	0.857389	0.003545	4
3	0.1	3	0.853266	0.000515	5
8	1	30	0.851028	0.002707	6
2	0.01	30	0.843330	0.002917	7
1	0.01	10	0.817832	0.001124	8
0	0.01	3	0.797166	0.000715	9
10	10	10	0.618080	0.124277	10
11	10	30	0.549338	0.210599	11
9	10	3	0.283476	0.003775	12

With only 2 parameters, we might want to visualize the grid-search as a heatmap. We need to transform our cv_results into a dataframe where:

the rows will correspond to the learning-rate values;
the columns will correspond to the maximum number of leaf;
the content of the dataframe will be the mean test scores.

pivoted_cv_results = cv_results.pivot_table(
    values="mean_test_score", index=["learning_rate"],
    columns=["max_leaf_nodes"])

pivoted_cv_results

max_leaf_nodes	3	10	30
learning_rate
0.01	0.797166	0.817832	0.843330
0.10	0.853266	0.866425	0.868063
1.00	0.857389	0.858863	0.851028
10.00	0.283476	0.618080	0.549338

We can use a heatmap representation to show the above dataframe visually.

import seaborn as sns

ax = sns.heatmap(pivoted_cv_results, annot=True, cmap="YlGnBu", vmin=0.7,
                 vmax=0.9)
ax.invert_yaxis()

../_images/parameter_tuning_grid_search_35_0.png

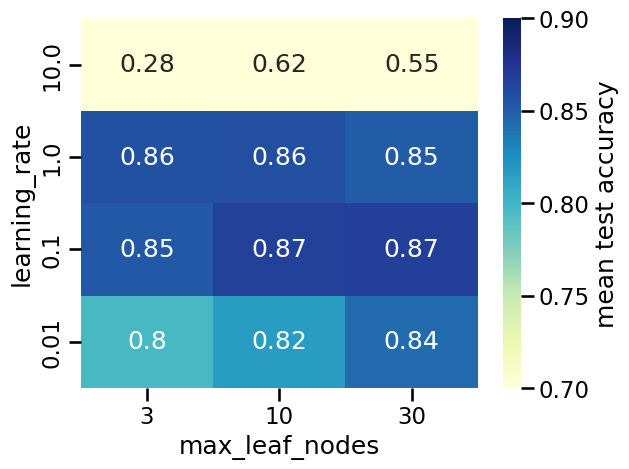
The above tables highlights the following things:

for too high values of learning_rate, the generalization performance of the model is degraded and adjusting the value of max_leaf_nodes cannot fix that problem;
outside of this pathological region, we observe that the optimal choice of max_leaf_nodes depends on the value of learning_rate;
in particular, we observe a “diagonal” of good models with an accuracy close to the maximal of 0.87: when the value of max_leaf_nodes is increased, one should decrease the value of learning_rate accordingly to preserve a good accuracy.

The precise meaning of those two parameters will be explained later.

For now we will note that, in general, there is no unique optimal parameter setting: 4 models out of the 12 parameter configurations reach the maximal accuracy (up to small random fluctuations caused by the sampling of the training set).

In this notebook we have seen:

how to optimize the hyperparameters of a predictive model via a grid-search;
that searching for more than two hyperparamters is too costly;
that a grid-search does not necessarily find an optimal solution.

Scikit-learn course

Hyperparameter tuning by grid-search¶

Our predictive model¶

Tuning using a grid-search¶