Limitation of selecting feature using a model

In this notebook, we want to show a limitation when using a machine-learning model to make a selection.

Indeed, one can inspect a model and find relative feature importances. For instance, the parameters coef_ for the linear models or feature_importances_ for the tree-based models carries such information. Therefore, this method works as far as the relative feature importances given by the model is sufficient to select the meaningful feature.

Here, we will generate a dataset that contains a large number of random features.

from sklearn.datasets import make_classification

data, target = make_classification(
    n_samples=5000,
    n_features=100,
    n_informative=2,
    n_redundant=5,
    n_repeated=5,
    class_sep=0.3,
    random_state=0,
)

First, let’s build a model which will not make any features selection.

from sklearn.ensemble import RandomForestClassifier

model_without_selection = RandomForestClassifier()

We will evaluate this model by a k-fold cross validation and store the results in a pandas dataframe.

import pandas as pd
from sklearn.model_selection import cross_validate

cv_results_without_selection = cross_validate(
    model_without_selection, data, target, cv=5
)
cv_results_without_selection = pd.DataFrame(cv_results_without_selection)

Then, we will build another model which will include a feature selection step based on a random forest and evaluate it as well with cross-validation.

from sklearn.pipeline import make_pipeline
from sklearn.feature_selection import SelectFromModel

feature_selector = SelectFromModel(RandomForestClassifier())
model_with_selection = make_pipeline(
    feature_selector, RandomForestClassifier()
)

cv_results_with_selection = cross_validate(
    model_with_selection, data, target, cv=5
)
cv_results_with_selection = pd.DataFrame(cv_results_with_selection)

We can compare the testing score of the two models. For this matter, we are combining results in a single dataframe.

cv_results = pd.concat(
    [cv_results_without_selection, cv_results_with_selection],
    axis=1,
    keys=["Without feature selection", "With feature selection"],
).swaplevel(axis="columns")

Finally, we can check the testing score of each the model.

import matplotlib.pyplot as plt

color = {"whiskers": "black", "medians": "black", "caps": "black"}
cv_results["test_score"].plot.box(color=color, vert=False)
plt.xlabel("Accuracy")
_ = plt.title("Limitation of using a random forest for feature selection")

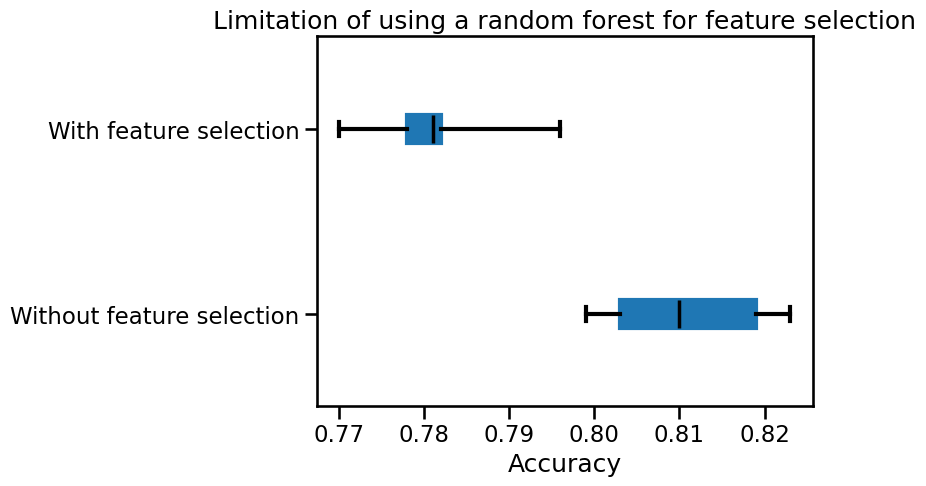
The model that selected a subset of feature is less performant than a random forest fitted on the full dataset.

We can rely on some aspects tackled in the notebook presenting the model inspection to explain this behaviour. The decision tree’s relative feature importance will overestimate the importance of random feature when the decision tree overfits the training set.

Therefore, it is good to keep in mind that feature selection relies on procedures making some assumptions, which can be perfectible.