Comparing model performance with a simple baseline#
In this notebook, we present how to compare the generalization performance of
a model to a minimal baseline. In regression, we can use the DummyRegressor
class to predict the mean target value observed on the training set without
using the input features.
We now demonstrate how to compute the score of a regression model and then compare it to such a baseline on the California housing dataset.
Note
If you want a deeper overview regarding this dataset, you can refer to the section named “Appendix - Datasets description” at the end of this MOOC.
from sklearn.datasets import fetch_california_housing
data, target = fetch_california_housing(return_X_y=True, as_frame=True)
target *= 100 # rescale the target in k$
Across all evaluations, we will use a ShuffleSplit cross-validation splitter
with 20% of the data held on the validation side of the split.
from sklearn.model_selection import ShuffleSplit
cv = ShuffleSplit(n_splits=30, test_size=0.2, random_state=0)
We start by running the cross-validation for a simple decision tree regressor. Here we compute the testing errors in terms of the mean absolute error (MAE) and then we store them in a pandas series to make it easier to plot the results.
import pandas as pd
from sklearn.tree import DecisionTreeRegressor
from sklearn.model_selection import cross_validate
regressor = DecisionTreeRegressor()
cv_results_tree_regressor = cross_validate(
regressor, data, target, cv=cv, scoring="neg_mean_absolute_error", n_jobs=2
)
errors_tree_regressor = pd.Series(
-cv_results_tree_regressor["test_score"], name="Decision tree regressor"
)
errors_tree_regressor.describe()
count 30.000000
mean 45.825742
std 1.269116
min 43.219154
25% 44.919116
50% 45.980396
75% 46.656999
max 48.345248
Name: Decision tree regressor, dtype: float64
Then, we evaluate our baseline. This baseline is called a dummy regressor.
This dummy regressor will always predict the mean target computed on the
training target variable. Therefore, the dummy regressor does not use any
information from the input features stored in the dataframe named data.
from sklearn.dummy import DummyRegressor
dummy = DummyRegressor(strategy="mean")
result_dummy = cross_validate(
dummy, data, target, cv=cv, scoring="neg_mean_absolute_error", n_jobs=2
)
errors_dummy_regressor = pd.Series(
-result_dummy["test_score"], name="Dummy regressor"
)
errors_dummy_regressor.describe()
count 30.000000
mean 91.140009
std 0.821140
min 89.757566
25% 90.543652
50% 91.034555
75% 91.979007
max 92.477244
Name: Dummy regressor, dtype: float64
We now plot the cross-validation testing errors for the mean target baseline and the actual decision tree regressor.
all_errors = pd.concat(
[errors_tree_regressor, errors_dummy_regressor],
axis=1,
)
all_errors
| Decision tree regressor | Dummy regressor | |
|---|---|---|
| 0 | 46.516950 | 90.713153 |
| 1 | 47.662282 | 90.539353 |
| 2 | 43.956121 | 91.941912 |
| 3 | 44.158180 | 90.213912 |
| 4 | 48.177636 | 92.015862 |
| 5 | 44.660312 | 90.542490 |
| 6 | 44.042069 | 89.757566 |
| 7 | 45.190667 | 92.477244 |
| 8 | 44.919805 | 90.947952 |
| 9 | 44.918887 | 91.991373 |
| 10 | 47.319935 | 92.023571 |
| 11 | 46.808933 | 90.556965 |
| 12 | 46.408011 | 91.539567 |
| 13 | 46.156584 | 91.185225 |
| 14 | 46.808616 | 92.298971 |
| 15 | 44.564747 | 91.084639 |
| 16 | 46.062039 | 90.984471 |
| 17 | 46.565664 | 89.981744 |
| 18 | 45.313654 | 90.547140 |
| 19 | 47.076979 | 89.820219 |
| 20 | 43.219154 | 91.768721 |
| 21 | 45.898754 | 92.305556 |
| 22 | 45.545971 | 90.503017 |
| 23 | 46.687445 | 92.147974 |
| 24 | 46.066053 | 91.386320 |
| 25 | 45.802517 | 90.815660 |
| 26 | 44.733016 | 92.216574 |
| 27 | 46.093279 | 90.107460 |
| 28 | 45.092768 | 90.620318 |
| 29 | 48.345248 | 91.165331 |
import matplotlib.pyplot as plt
import numpy as np
bins = np.linspace(start=0, stop=100, num=80)
all_errors.plot.hist(bins=bins, edgecolor="black")
plt.legend(bbox_to_anchor=(1.05, 0.8), loc="upper left")
plt.xlabel("Mean absolute error (k$)")
_ = plt.title("Cross-validation testing errors")
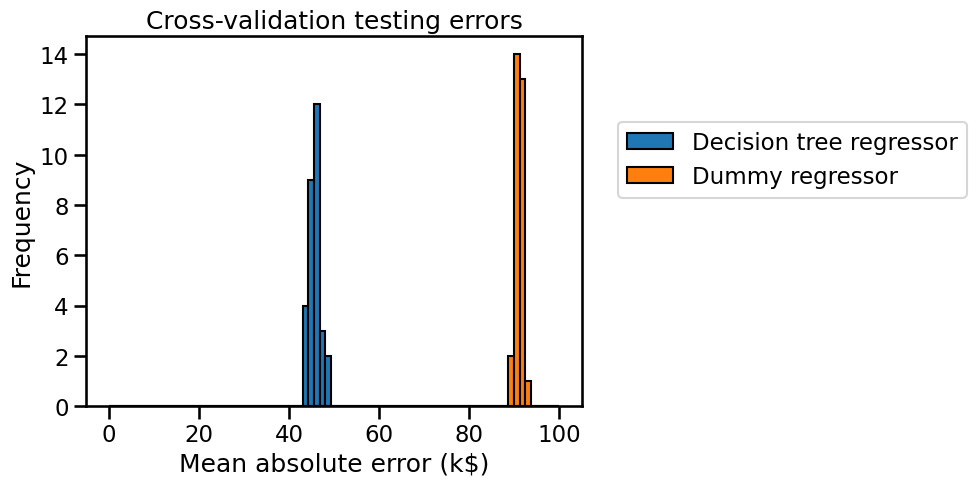
We see that the generalization performance of our decision tree is far from being perfect: the price predictions are off by more than 45,000 US dollars on average. However it is much better than the mean price baseline. So this confirms that it is possible to predict the housing price much better by using a model that takes into account the values of the input features (housing location, size, neighborhood income…). Such a model makes more informed predictions and approximately divides the error rate by a factor of 2 compared to the baseline that ignores the input features.
Note that here we used the mean price as the baseline prediction. We could have used the median instead. See the online documentation of the sklearn.dummy.DummyRegressor class for other options. For this particular example, using the mean instead of the median does not make much of a difference but this could have been the case for dataset with extreme outliers.
Finally, let us see what happens if we measure the test score using \(R^2\) instead of the mean absolute error:
result_dummy = cross_validate(
dummy, data, target, cv=cv, scoring="r2", return_train_score=True, n_jobs=2
)
r2_train_score_dummy_regressor = pd.Series(
result_dummy["train_score"], name="Dummy regressor train score"
)
r2_train_score_dummy_regressor.describe()
count 30.0
mean 0.0
std 0.0
min 0.0
25% 0.0
50% 0.0
75% 0.0
max 0.0
Name: Dummy regressor train score, dtype: float64
The \(R^2\) score is always 0. It can be shown that this is always the case, because of its mathematical definition. If you are interested in the proof, unfold the dropdown below.
Mathematical explanation
Recall that the \(R^2\) score is defined as:
\( R^2 = 1 - \frac{\sum_i (y_i - \hat{y}_i)^2}{\sum_i (y_i - \bar{y})^2} \)
But our model always predicts the mean, i.e. for all \(i\), \(\hat{y}_i = \bar{y}\), so:
\( R^2 = 1 - \frac{\sum_i (y_i - \hat{y}_i)^2}{\sum_i (y_i - \bar{y})^2} = 1 - \frac{\sum_i (y_i - \bar{y} )^2}{\sum_i (y_i - \bar{y})^2} = 1 - 1 = 0. \)
This helps put your model’s \(R^2\) score in perspective: if your model has an
\(R^2\) score higher than 0 then it performs better than a DummyRegressor with
strategy="mean"; similarly, if the \(R^2\) score is lower than 0 then your
model is worse than the dummy regressor. For the test score, we observe
something similar, but with an additional effect coming from the dataset
variations: the mean target value measured on the testing set is slightly
different from the mean target value measured on the training set.
r2_test_score_dummy_regressor = pd.Series(
result_dummy["test_score"], name="Dummy regressor test score"
)
r2_test_score_dummy_regressor.describe()
count 3.000000e+01
mean -2.203750e-04
std 3.572610e-04
min -1.797131e-03
25% -2.753534e-04
50% -1.083489e-04
75% -3.344120e-05
max -1.015390e-07
Name: Dummy regressor test score, dtype: float64
In conclusion, \(R^2\) is a normalized metric, which makes it independent of the physical unit of the target variable, unlike MAE. A \(R^2\) score of 0.0 is the performance of a model that always predicts the mean observed value of the target, while 1.0 corresponds to a model that predicts exactly the observed target variable for each given input observation. Notice that it is only possible to reach 1.0 if the target variable is a deterministic function of the available input features. In practice, external factors often introduce variability in the target that cannot be explained by the available features. Therefore, the \(R^2\) score of an optimal model is typically less than 1.0, not due to a limitation of the machine learning algorithm itself, but because the chosen input features are fundamentally not informative enough to deterministically predict the target.
Overall, \(R^2\) represents the proportion of the target’s variability explained by the model, while MAE, which retains the physical units of the target, can be helpful for reporting errors in those units.

